原帖由 阳3光6飞0狐 于 2008-10-7 18:27 发表
这张图什么意思啊?我看不太懂啊除了旁边的表,还有什么意思啊?

67531
 除了旁边的表,还有什么意思啊?
除了旁边的表,还有什么意思啊?





原帖由 catlet 于 2008-10-8 09:32 发表
正四面体
正六面体
http://www.swxl.com.cn/math ...
 ,对于以两个这样的运动相继施行作为乘法构成群,称为多面体群。由几何学可知,正多面体只有5种,即正四面体、正六面体、正八面体、正十二面体、正二十面体。于是有正四面体群、正六(八)面体群、正十二(二十)面体群等三种群。
,对于以两个这样的运动相继施行作为乘法构成群,称为多面体群。由几何学可知,正多面体只有5种,即正四面体、正六面体、正八面体、正十二面体、正二十面体。于是有正四面体群、正六(八)面体群、正十二(二十)面体群等三种群。
 与A点连结的直线AO
与A点连结的直线AO 为轴,如图1[正四面体]
为轴,如图1[正四面体] ,将正四面体A-BCD 按反时针方向绕 AO
,将正四面体A-BCD 按反时针方向绕 AO 轴作角度为2
轴作角度为2 /3与4
/3与4 /3的旋转
/3的旋转 显然,这两个旋转运动分别对应于置换(BCD)与(BDC),且使正四面体在其运动前后占有同一空间位置
显然,这两个旋转运动分别对应于置换(BCD)与(BDC),且使正四面体在其运动前后占有同一空间位置 仿此,连结
仿此,连结  点与正三角形ACD的中心
点与正三角形ACD的中心
 的直线BO
的直线BO 为轴作角度为2
为轴作角度为2 /3 与 4
/3 与 4 /3的旋转,这两个旋转运动分别对应于置换(ACD)与(ADC),并使正四面体在运动前后占有同一空间位置。同理,与置换(ABD)及(ADB),(ABC)及(ACB)所对应的旋转,也使正四面体在运动前后占有同一空间位置。综上所述共有8个三项循环:(BCD),(BDC),(ACD),(ADC),(ABD),(ADB),(ABC),(ACB)。它们分别对应的旋转都是使正四面体占有同一空间位置的运动。再以正四面体A-BCD的3对对边之中点联线为旋转轴, 作角度为
/3的旋转,这两个旋转运动分别对应于置换(ACD)与(ADC),并使正四面体在运动前后占有同一空间位置。同理,与置换(ABD)及(ADB),(ABC)及(ACB)所对应的旋转,也使正四面体在运动前后占有同一空间位置。综上所述共有8个三项循环:(BCD),(BDC),(ACD),(ADC),(ABD),(ADB),(ABC),(ACB)。它们分别对应的旋转都是使正四面体占有同一空间位置的运动。再以正四面体A-BCD的3对对边之中点联线为旋转轴, 作角度为 的3个旋转,它们分别对应于置换(AB)(CD),(AC)(BD),(AD)(BC),并使正四面体占有同一空间位置。以
的3个旋转,它们分别对应于置换(AB)(CD),(AC)(BD),(AD)(BC),并使正四面体占有同一空间位置。以 表示旋转角为0的旋转即不动旋转,显然,
表示旋转角为0的旋转即不动旋转,显然, 是使正四面体占有同一空间位置的运动。总计共得12个旋转运动。除此之外再没有其他运动可保持正四面体占有空间位置不变。这样的12个运动构成群,称为正四面体群。它与4个文字A、
是使正四面体占有同一空间位置的运动。总计共得12个旋转运动。除此之外再没有其他运动可保持正四面体占有空间位置不变。这样的12个运动构成群,称为正四面体群。它与4个文字A、 、
、 、
、 上的四次交错群[151-02]
上的四次交错群[151-02]
 同构,因此,四次交错群[151-02]
同构,因此,四次交错群[151-02]
 又称为正四面体群。
又称为正四面体群。 ,如图2a[正八面体]
,如图2a[正八面体] ,其各个面都是正三角形,顺次联结各面的中心
,其各个面都是正三角形,顺次联结各面的中心 ,
, ,
, ,
, ,
, ,
, ,
, ,
, 即得一个正六面体
即得一个正六面体


 -
-


 ,如图2b[正六面体]
,如图2b[正六面体] 。对于正八面体A-BCDE-
。对于正八面体A-BCDE- 分别以其 3条对角线AF,BD,CE为旋转轴,作
分别以其 3条对角线AF,BD,CE为旋转轴,作 /2,
/2, ,3
,3 /2的旋转,共有9个旋转运动。它们都能使正八面体占有同一空间位置,同时使正六面体也占有同一空间位置。
/2的旋转,共有9个旋转运动。它们都能使正八面体占有同一空间位置,同时使正六面体也占有同一空间位置。 /3、2
/3、2 /3的旋转,共有8个这样的运动。它们使正八面体,也使正六面体不变更所占的空间位置。再以正八面体的6对两平行棱的中点联线为轴作角度为
/3的旋转,共有8个这样的运动。它们使正八面体,也使正六面体不变更所占的空间位置。再以正八面体的6对两平行棱的中点联线为轴作角度为 的旋转,共有6个旋转运动。它们使正八面体,并因之使正六面体不变更占有的空间位置。加上不动旋转
的旋转,共有6个旋转运动。它们使正八面体,并因之使正六面体不变更占有的空间位置。加上不动旋转 ,于是,使正八面体或正六面体不变更占有的空间位置的旋转运动,总计有24个,且只有这24个。这样的24个运动构成群,称为正八面体群或正六面体群。它与四次对称群[151-01]
,于是,使正八面体或正六面体不变更占有的空间位置的旋转运动,总计有24个,且只有这24个。这样的24个运动构成群,称为正八面体群或正六面体群。它与四次对称群[151-01]
 同构,所以正八面体群与正六面体群是一致的,都是 4次对称群[151-01]
同构,所以正八面体群与正六面体群是一致的,都是 4次对称群[151-01]
 。 有时把四次对称群称为正八面体群或正六面体群。
。 有时把四次对称群称为正八面体群或正六面体群。 )。因此,正十二面体群与正二十面体群是一致的。以正十二面体的 6对相对面的中心连线为轴作2
)。因此,正十二面体群与正二十面体群是一致的。以正十二面体的 6对相对面的中心连线为轴作2 /5,4
/5,4 /5,6
/5,6 /5,8
/5,8 /5的旋转,这样的旋转共有24个。以10对相对顶点的连线为轴作 2
/5的旋转,这样的旋转共有24个。以10对相对顶点的连线为轴作 2 /3、4
/3、4 /3的旋转,这样的旋转共有20个。以15对相对对边的中心连线为轴作
/3的旋转,这样的旋转共有20个。以15对相对对边的中心连线为轴作 的旋转, 这样的旋转共有15个
的旋转, 这样的旋转共有15个 不动旋转
不动旋转 一个。于是,使正十二面体或正二十面体不变更占有的空间位置的旋转共有60个,且只有这60个。这样的60个旋转构成群,称为正十二面体群或正二十面体群。它与5次交错群[151-02]
一个。于是,使正十二面体或正二十面体不变更占有的空间位置的旋转共有60个,且只有这60个。这样的60个旋转构成群,称为正十二面体群或正二十面体群。它与5次交错群[151-02]
 同构。
同构。

 I like
I like
 ,那么有
,那么有 根据构造方法的不同,幻方可以分成三类:奇数阶幻方、4M阶幻方和4M + 2阶幻方,其中M为自然数,2阶幻方不存在。幻方构造法主要有:连续摆数法、阶梯法(楼梯法)、奇偶数分开的菱形法、对称法、对角线法、比例放大法、斯特雷奇法、LUX法、拉伊尔法(基方、根方合成法)、镶边法、相乘法、幻方模式等。
根据构造方法的不同,幻方可以分成三类:奇数阶幻方、4M阶幻方和4M + 2阶幻方,其中M为自然数,2阶幻方不存在。幻方构造法主要有:连续摆数法、阶梯法(楼梯法)、奇偶数分开的菱形法、对称法、对角线法、比例放大法、斯特雷奇法、LUX法、拉伊尔法(基方、根方合成法)、镶边法、相乘法、幻方模式等。 等数放在右上方格中。
等数放在右上方格中。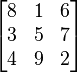 | 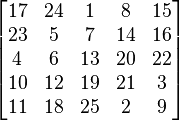 |  |
| 3阶 | 5阶 | 9阶 |
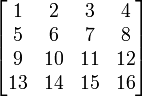


 和
和 这些数安排在外圈格子内,但要使相对两数之和等于16m(m + 1) + 5。对于m = 1这些数是:1,2,3,4,5,6,7,8,9,10;27,28,29,30,31,32,33,34,35,36。
这些数安排在外圈格子内,但要使相对两数之和等于16m(m + 1) + 5。对于m = 1这些数是:1,2,3,4,5,6,7,8,9,10;27,28,29,30,31,32,33,34,35,36。
 罗总玩双色球跟你投注啊
罗总玩双色球跟你投注啊
 ~~
~~




 ~~
~~







| 欢迎光临 【阳光飞狐__与财富同行】 (http://bbs.88158.cn/) | Powered by Discuz! X3.2 |